The  Non-Mathematician's  Guide  To  Basic  Valveless  Pulsejet  Theory © 2008 Larry Cottrill                                                                   by Larry Cottrill   25 Sep 2008 Subtopic 03.01 First Principles: The Kadenacy Effect Perhaps the simplest reaction "engine" is an inflated latex balloon: You pressurize it by blowing air into it, pinching the inflation neck closed as you go along; then, when you think it's "ready" (or you're too tired to inflate it further), you release it. The balloon zooms around in unpredictably changing directions and finally flops down somewhere and just lies there in a heap. It doesn't take too much imagination to see that the pressure in the balloon has gradually declined as the balloon was flying around, until it finally reached the outside air pressure. It is an extremely crude form of model rocket; as such, it is a "one shot" device until it is "re-loaded". What would happen if we had some automatic way of re-inflating the balloon back to its original pressure while it was still in flight? If this mythical mechanism was very efficient (and very light weight!) we would have an "engine" that would keep itself going indefinitely! Of course, we would still have the problem that our balloon engine has no good sense of direction, but that could be solved aerodynamically, as it is with the fins on a real model rocket. Strange as it may seem, it is entirely possible to make a device that blasts air out to create rocket-like "thrust" and then re-pressurizes itself! It turns out that a container like a balloon can't do this because it is so big and the outlet "nozzle" is so small; under those conditions, the air pressure just gradually runs down until it's no greater than the air pressure around it. However, if the air reservoir is made of rigid material instead of a flexible membrane, and if it vents through a much larger nozzle, the action is much more complex: First, the air rushes out MUCH faster (due to the larger opening), and so the pressure drops much faster. Second, when the air in the reservoir reaches the outdoor air pressure, the air doesn't stop rushing out -- the high speed of the outflowing air keeps it moving, and the air pressure inside continues to drop! Third, eventually the pressure difference between the inside air and outside air becomes so great that outflow really does slow to a stop. And fourth, at this point, the now reversed pressure difference causes air to begin flowing back into the reservoir to re-fill it. But wait, there's more! Just as the outflow of air didn't stop when the pressures were equal, the inflow refuses to stop there, too! So, eventually, the action continues until there is once again higher pressure in the reservoir until a point is reached where the flow is brought to a halt. Once you really visualize this back-and-forth pressure cycling, it's really quite amazing -- it's actually a kind of reciprocating air pump without any moving parts! What I've just described is known as "Kadenacy Action" or "the Kadenacy Effect", named after physicist Michael Kadenacy who studied the effect in depth in the 1930s (though it was first discovered by the great Dutch physical scientist Christiaan Huygens back in the 1600s). If the movement of air were a "lossless" (100 percent efficient) phenomenon, this pumping action would result in the original high pressure in the reservoir being fully restored, and the cycle would keep going on forever (a "perpetual motion machine" with no moving parts!). Of course, in reality, it doesn't work out this way -- aerodynamic properties like drag and turbulence take their toll on each cycle, so the restored pressure is always lower than the original value, and the process "winds down". It is possible to graph the pressure at the base of a real reservoir once the initial pressure has been set and the nozzle has been opened up -- as an example, we'll use a so-called "flashlight shaped" vessel (a short, fat reservoir we'll call the "chamber", a short transition cone called the "nozzle" and a much longer tubular duct we'll refer to as the "pipe" -- all having perfectly circular cross sections and all lying on a common centerline): The left end is fully closed (shown as a slightly domed plate); the right end is fully open. 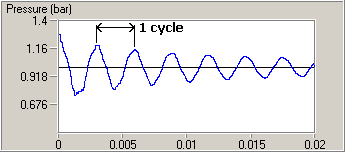And here is our first example of the changing pressure at the closed "front" of the chamber (near the very left end in the drawing above), graphed over a .02 second time interval: This vessel shape is important because it is the basic shape of the main body of one of the simplest forms of pulsejet. I chose it, though, because the pressure in the chamber graphs over time as a very "clean" shape -- almost a perfect damped sine curve. The term "damped" refers simply to the fact that the power (magnitude) of the curve "winds down" over time, as can be clearly seen here. That fact is clear evidence that we aren't looking at a lossless process. Remember that this is a graph of air pressure at the closed front end of the chamber, which happens to be the location of the largest pressure swings in the vessel. In the next subtopic, we'll look at these pressure changes in greater detail and see how they take the form of an "acoustic wave" that moves back and forth along the interior length of the vessel. Next subtopic:   Kadenacy "Hangs ten" Go back to select another subtopic